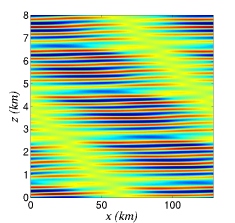
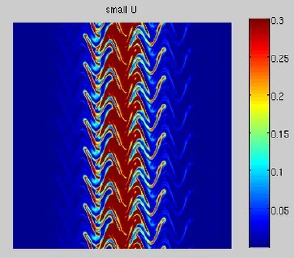
Multifractal structure of the vorticity gradient squared (click to enlarge)
In the forward enstrophy cascade
range, a linear drag causes the power-law exponent of the energy
spectrum to become steeper than the classical value of -3. Moreover,
the system becomes intermittent.
These are the results of the non-uniform stretching in the fluid
coupled with a linear drag. A theory based on finite-time Lyapunov
exponent is used to predict the energy spectrum exponent. The
intermittency is quantified by:
(i) the anomalous scaling of the vorticity structure functons,(ii) the scale dependence of the probability density of the vorticity increments,
(iii) the multifractality of the viscous enstrophy dissipation.
Intermittency in two-dimensional turbulence with drag, Phys. Rev. E 71, 066313 (2005) [PDF]
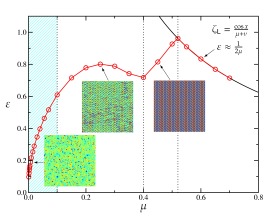
Energy
injection rate vs. drag coefficient (click to enlarge)
In the inverse energy cascade
range, a linear drag introduces a cutoff in the energy spectrum at
large scales rather than changing the power-law exponent significantly
from its classical value of -5/3. In this regime, we focus on the
dependence of the energy injection
rate on drag. The energy injection rate plays a crucial role in
Kraichnan's phenomenolgy, it is also of practical importance in many
engineering and meteorological applications. Our numerical simulations
reveal a new scaling regime in which the energy injection rate has a
power-law dependence on the drag coefficient, with a scaling exponent
of 1/3. Such scaling stems from
the nonlocal interaction between the small-scale forced mode and the
large-scale eddies.
Forced-dissipative two-dimensional turbulence: a scaling regime controlled by drag, Phys. Rev. E 79, 045308(R) (2009) [PDF]
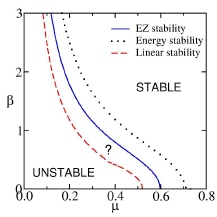
Stability curves by various
methods (click to enlarge)
We also study the stability of a two-dimensional
flow forced by a sinusoidal body force (Kolmogorov flow) on a β-plane.
We focus on the case where drag is the main dissipative mechanism.
Linear instability theory determines the part of the parameter space
where the flow is unstable to infinitesimal perturbations. On the other
hand, nonlinear stability analysis, establish the region in which the
flow is stable to arbitrary perturbations. Observing that there exists
a constraint on the time evolution of the difference between the energy
and enstrophy, we develop a new nonlinear stability method, the
energy-enstrophy (EZ) method, which proves nonlinear stability in a
larger portion of the parameter space than the traditional energy
method.
Energy-enstrophy stability of β-plane Kolmogorov flow with drag, Phys. Fluids 20, 084102 (2008) [PDF]
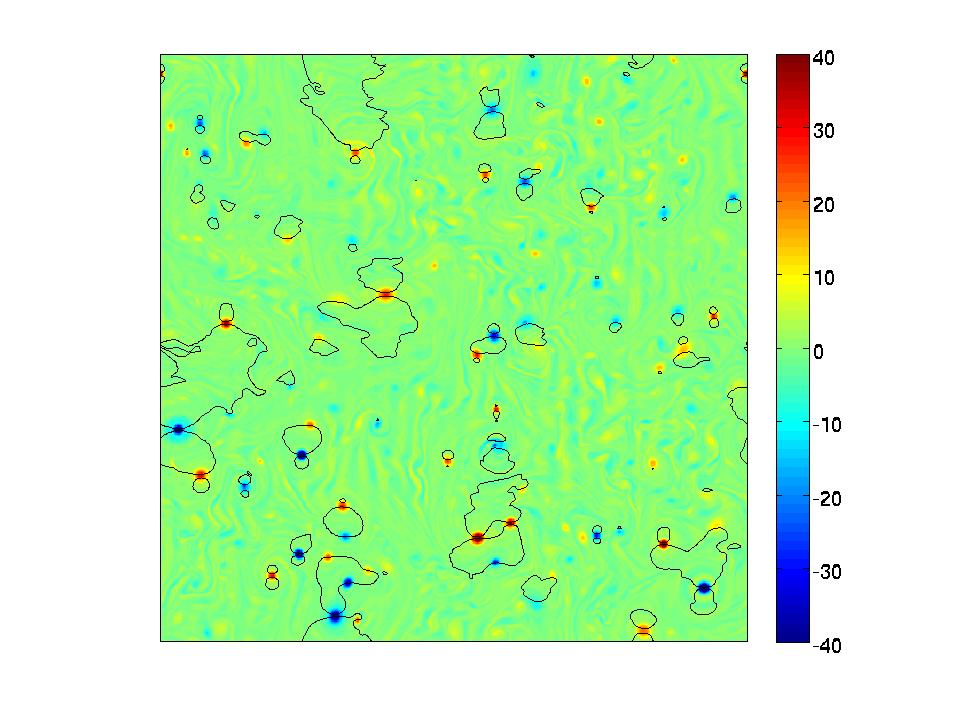
There have been a lot of interest in the one-point velocity statistics of forced two-dimensional turbulence. Specifically, is the velocity probability density function (PDF) Gaussian or non-Gaussian?
It turns out the answer depends on the large-scale dissipation that is required to remove the energy
injected by the forcing (at the small scales). For hypo-drag or hypo-viscosity, where damping only occurs
at the large-scale modes, the velocity PDF is non-Gaussian due to the strong vortices present in the
system. On the other hand, with the physically motivated linear (Ekman) drag or quadratic drag, the
velocity PDF is close to Gaussian and somewhat surprisingly, the background vorticity is an important
factor in shaping the velocity PDF even though vortices are visually dominant in the flow. Further information on the relation between the velocity PDF and the large-scale drag is revealed by the vortex statistics obtained from a vortex census algorithm.
The movie on the right shows that the high velocity regions (which contirbute to the tail of the velocity PDF) comes from the background vorticity for linear drag but are associated with the vortices for hypo-drag.
The movie on the right shows that the high velocity regions (which contirbute to the tail of the velocity PDF) comes from the background vorticity for linear drag but are associated with the vortices for hypo-drag.
Non-universal velocity probability densities in forced two-dimensional turbulence: the effect of large-scale dissipation, Phys. Fluids 22, 115102 (2010) [PDF]